常见排序算法

2020-09-05

字数统计: 1.8k字 | 阅读时长: 8分钟

背景

人类社会需要秩序，顺序从某个角度而言是秩序的一种。在算法的世界里，顺序具有重要地位。那该将一些混乱无序的数据变成有序的呢？以下是一些经典算法实现，完整代码请用神奇的传送门~。

常见排序

1，排序总结图

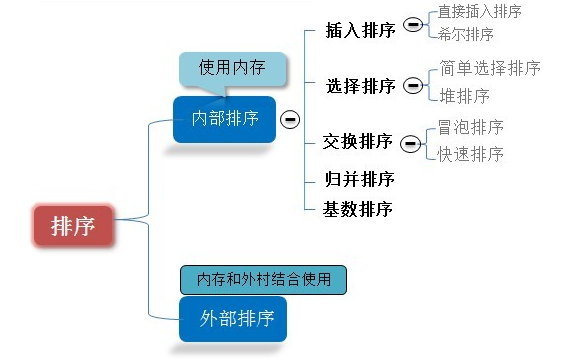
2，排序算法分析图

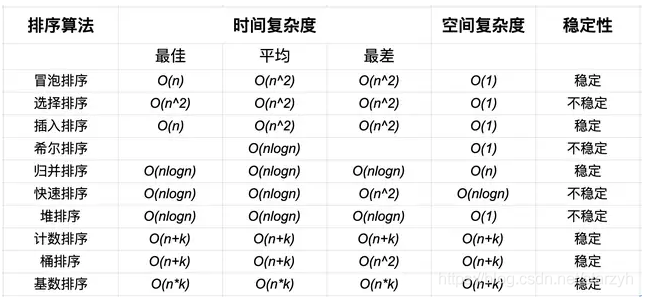
一，插入排序

Insertion Sort

（一）直接插入排序

Straight Insertion Sort

基本思想

将一个记录插入到已排序好的有序表中，从而得到一个新，记录数增1的有序表。即：先将序列的第1个记录看成是一个有序的子序列，然后从第2个记录逐个进行插入，直至整个序列有序为止。

代码实现

void StraightInsertionSort(int *arr)
{
    int i, j;
    /*
    for (i=2; i<SIZE; i++)
    {
        if (arr[i] < arr[i-1])
        {
            arr[0] = arr[i];  //设置数组首元素为哨兵
            for (j=i-1; arr[j]>arr[0]; j--)
            {
                arr[j+1] = arr[j];
            }
            arr[j+1] = arr[0];
        }
    }
    */
   for (i=1; i<SIZE; i++) //首元素从第二个开始
    {
        if (arr[i] < arr[i-1])
        {
            int value = arr[i];  //没有设置数组首元素为哨兵
            for (j=i-1; j>=0 && arr[j]>value; j--)
            {
                arr[j+1] = arr[j];
            }
            arr[j+1] = value;
        }
    }
}

（二）折半排序

基本思想

在直接插入排序的基础上，在有序的子序列中运用折半查找确定插入位置。

代码实现

void BInsertSort(int *arr)
{
    int i, j, m, value, low, high;
    for (i=1; i<SIZE; i++)
    {
        low = 0;
        high = i-1;
        if (arr[i] < arr[i-1])
        {
            value = arr[i];
            while (low <= high)
            {
                m = (low+high)/2;
                if (arr[m]>value) 
                    high = m-1;
                else 
                    low = m+1;
            }
            for (j=i-1; j>=high+1; j--)
            {
                arr[j+1] = arr[j];
            }
            arr[j+1] = value; //arr[high+1] = value;
        }
    }
}

（三）希尔排序

基本思想

先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序，待整个序列中的记录“基本有序”时，再对全体记录进行依次直接插入排序。

代码实现

void shellSort(int *arr, int incresement)
{
    int i, j;

    for (i=incresement; i<SIZE; i++)
    {
        if (arr[i] < arr[i-incresement])
        {
            int value = arr[i];
            for (j=i-incresement; j>=0&&arr[j]>value; j=j-incresement)
            {
                arr[j+incresement] = arr[j];
            }
            arr[j+incresement] = value;
        }
    }
}

二，选择排序

Selection Sort

（一）简单选择排序

Simple Selection Sort

基本思想

在要排序的一组数中，选出最小（或者最大）的一个数与第1个位置的数交换；然后在剩下的数当中再找最小（或者最大）的与第2个位置的数交换，依次类推，直到第n-1个元素（倒数第二个数）和第n个元素（最后一个数）比较为止。

代码实现

void SimpleSelectSort(int *arr)
{
    int i, j, min, temp;
    for (i=0; i<SIZE-1; i++)
    {
        min = i;
        for (j=i+1; j<SIZE; j++)
        {
            if (arr[min]>arr[j])
            {
                min = j;
            }
        }
        if (min != i)
        {
            temp = arr[min];
            arr[min] = arr[i];
            arr[i] = temp;
        }
    }
}

（二）堆排序

Heap Sort

基本思想

堆的定义如下：具有n个元素的序列（k1,k2,…,kn),当且仅当满足ai>=a2i+1,ai>=a2i或者ai<=a2i+1,ai<=a2i时称之为堆。

可以将堆看做是一个完全二叉树。并且，每个结点的值都大于等于其左右孩子结点的值，称为大顶堆；或者每个结点的值都小于等于其左右孩子结点的值，称为小顶堆。

将待排序列表构造成一个最大堆，作为初始无序堆（即初始无序列表）

将堆顶元素（最大值）与堆尾元素互换

将该堆（无序区）尺寸缩小1，并对缩小后的堆重新调整为最大堆形式

重复上述步骤，直至堆（无序区）的尺寸变为1，此时排序完成

代码实现

void heapify(int *tree, int n, int i)
{
    if (i >= n)
    {
        return;
    }
    int c1 = i*2 + 1;
    int c2 = i*2 + 2;
    int max = i;
    if (c1<n && tree[c1]>tree[max])
        max = c1;
    if (c2<n && tree[c2]>tree[max])
        max = c2;
    if (max != i)
    {
        swap(tree, i, max);
        heapify(tree, n, max);
    }
}

void buildHeap(int *tree, int n)
{
    int last_node = n-1;
    int last_node_parent = (last_node-1)/2; 
    for (int i=last_node_parent; i>=0; i--)
    {
        heapify(tree, n, i);
    }
}

void heapSort(int *tree, int n)
{
    buildHeap(tree, n);
    for (int i=n-1; i>=0; i--)
    {
        swap(tree, i, 0);
        heapify(tree, i, 0);
    }
}

void swap(int *tree, int i, int j)
{
    int temp = tree[i];
    tree[i] = tree[j];
    tree[j] = temp;
}

三，交换排序

Swap Sort

（一）冒泡排序

Bubble Sort

基本思想

重复的遍历（走过）待排序的一组数字（通常是列表形式），依次比较两个相邻的元素（数字），若它们的顺序错误则将它们调换一下位置，直至没有元素再需要交换为止。

每遍历一次列表，最大（或最小）的元素会经过交换一点点”浮“到列表的一端（顶端），所以形象的称这个算法为冒泡算法。

代码实现

void BubbleSort(int *arr)
{
    int i, j, temp, flag;
    for (i=0; i<SIZE-1; i++)
    {
        flag = 0;
        for (j=0; j<SIZE-i-1; j++)
        {
            if (arr[j] > arr[j+1])
            {
                temp = arr[j];
                arr[j] = arr[j+1];
                arr[j+1] = temp;
                flag = 1;
            }
        }
        if (flag == 0)
            break;
    }
}

（二）快速排序

Quick Sort

基本思想

通过一趟排序将待排序列表分割成独立的两部分，其中一部分的所有元素都比另一部分小，然后再按此方法将独立的两部分分别继续重复进行此操作，这个过程我们可以通过递归实现，从而达到最终将整个列表排序的目的。

代码实现

void quicksort(int *arr, int low, int high)
{
    int pos;
    if (low < high)
    {
        pos = findpos(arr, low, high);
        quicksort(arr, low, pos-1);
        quicksort(arr, pos+1, high);
    }
}

int findpos(int *arr, int low, int high)
{
    int value = arr[low];
    while (low < high)
    {
        while (low<high && arr[high]>=value)
        {
            high--;
        }
        arr[low] = arr[high];
        while (low<high && arr[low]<=value)
        {
            low++;
        }
        arr[high] = arr[low];
    }
    arr[low] = value;

    return low;
}

四，归并排序

Merge Sort

基本思想

是将两个（或两个以上）有序表合并成一个新的有序表，即把待排序序列分为若干个子序列，每个子序列是有序的。然后再把有序子序列合并为整体有序序列。

代码实现

void Merge(int *arr, int left, int middle, int right)
{
    int left_size = middle-left;
    int right_size = right-middle+1;
    int left_arr[left_size];
    int right_arr[right_size];
    int i, j, k;
    for (i=left; i<middle; i++)
    {
        left_arr[i-left] = arr[i];
    }
    for (j=middle; j<=right; j++)
    {
        right_arr[j-middle] = arr[j];
    }
    
    //对两个子数组元素进行合并
    i=0; j=0; k=left;
    while (i<left_size && j<right_size)
    {
        if (left_arr[i] < right_arr[j])
        {
            arr[k] = left_arr[i];
            i++;
            k++;
        }
        else
        {
            arr[k] = right_arr[j];
            j++;
            k++;
        }
    }
    //将剩余数据填入源数组中
    while (i < left_size)
    {
        arr[k] = left_arr[i];
        i++;
        k++;
    }
    while (j < right_size)
    {
        arr[k] = right_arr[j];
        j++;
        k++;
    }
}

void MergeSort(int *arr, int left, int right)
{
    if (left >= right)
        return;
    else
    {
        int middle = (left+right)/2;
        MergeSort(arr, left, middle);
        MergeSort(arr, middle+1, right);
        Merge(arr, left, middle+1, right);
    }
}